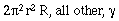Table of Contents
APPENDIX B
PARAMETERS OF HABITABILITY
In a rotating habitat in space three factors affect the area and
volume available for residence. Due to physiological considerations
living and sleeping are confined for a large portion of the day to
a volume where the change in pseudogravity, g, is less than some
amount,  g, which experience must
determine. The habitable volume is that volume where
g, which experience must
determine. The habitable volume is that volume where  g/g is less than or equal to some number
which the study group calls the habitability parameter,
g/g is less than or equal to some number
which the study group calls the habitability parameter, 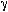 =
=  g/g. It is not
inconceivable, for example, that ways may be found to live safely
and comfortably through the entire range from 0 to 1 g. In that
case
g/g. It is not
inconceivable, for example, that ways may be found to live safely
and comfortably through the entire range from 0 to 1 g. In that
case 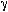 would equal 1, and the entire volume of the
space colony is habitable.
would equal 1, and the entire volume of the
space colony is habitable.
Projected Area
City planners and architects design human habitation in terms of
the surface area on which buildings may be constructed. In the
kinds of habitats discussed in this study, the curvature of
surfaces on which colonists might live is often pronounced. It
seems reasonable to define available surface area as the projection
of area onto a plane perpendicular to the direction of the
pseudogravity. In a torus the projected area is a strip through the
diameter of the tube of the torus (see
fig. 4-17). If the minor radius is r and the major radius is R.
the projected area for a torus is  .
This is just
.
This is just 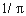 the total skin area of a
torus. Note that if the torus is spun so that there is 1 g of
pseudogravity at the outermost surface, and if the aspect ratio,
the total skin area of a
torus. Note that if the torus is spun so that there is 1 g of
pseudogravity at the outermost surface, and if the aspect ratio,
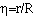 , is greater than the habitability
parameter,
, is greater than the habitability
parameter, 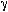 , the plane of projected area is
outside the habitable volume. For all the cases considered,
, the plane of projected area is
outside the habitable volume. For all the cases considered,
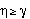 , and the above formula is sufficient. For a
rotating sphere the projected plane of usable area is the surface
of a cylinder inscribed in the sphere (see
fig. 4-18). The surface of this cylinder should not be more
than
, and the above formula is sufficient. For a
rotating sphere the projected plane of usable area is the surface
of a cylinder inscribed in the sphere (see
fig. 4-18). The surface of this cylinder should not be more
than 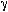 R above the surface of the sphere. The
projected area then is
R above the surface of the sphere. The
projected area then is
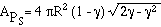
At 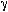 = 0.29 this expression has a maximum
= 0.29 this expression has a maximum
 .
.
Consequently for  the expression for
the maximum can be used. (Alternatively, for smaller
the expression for
the maximum can be used. (Alternatively, for smaller 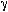 , the habitat might be spun to produce 1 g at
, the habitat might be spun to produce 1 g at
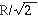 to maximize the available area). For a cylinder
of radius R and length L the projected area is just the surface
area
to maximize the available area). For a cylinder
of radius R and length L the projected area is just the surface
area 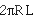 <.
<.
Table 4-6 summarizes the expressions
for projected area in different geometries.
Habitable Volume
Although projected area represents an important concept in
conventional architectural thinking, the available volume in the
habitat may be more relevant in specifying the apparent population
density and the quality of life. Habitable volume is defined as
that volume in which the pseudogravity does not vary more than the
specified amount,  g, from the
nominal value of g. Consequently, habitable volume depends on
g, from the
nominal value of g. Consequently, habitable volume depends on
 g/g.
g/g.
For a cylinder of length L and radius of rotation R. the
habitable volume is the annulus between R and (1 - 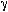 R. In a sphere with a pseudogravity no
greater than 1 g on its surface, habitable volume is the figure of
revolution of the shaded area (as for the sphere in fig.4-18)
R. In a sphere with a pseudogravity no
greater than 1 g on its surface, habitable volume is the figure of
revolution of the shaded area (as for the sphere in fig.4-18)
In a torus with 1 g at its outermost circumference, habitable
volume is the shaded area of the tube revolved around the axis of
rotation. The formulas for these volumes are given in table
4-6.
TABLE 4-6 (gif format)
TABLE4-6.- PROJECTED AREAS AND HABITABLE VOLUMES
| Geometry |
Projected area,
Ap |
Habitable volume,
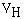 |
| Cylinder |
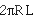 |
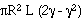 |
| Sphere |
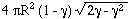 |
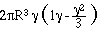 |
Cylinder and
spherical endcaps |
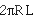
+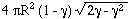 |
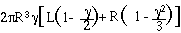 |
| Torus |
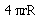 |
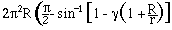
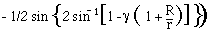
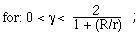 < <
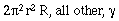 |
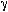 =
=  g/g
g/g
r= minor radius of torus
R= radius of rotation
L= length of cylinder
Area and Volume Requirements
The study group determined that a reasonable standard of
projected area is 67 m^2/person. Also, a detailed inventory of
structures and facilities required for individual and community
life suggests that habitable volume should be about 1740
m^3/person. Consequently, a habitat, or a collection of habitats,
suitable for a given population of 10,000 people, must provide an
area of 670,000 m^2 and a volume of 17,400,000 m^3. These numbers
determine the geometry in a fundamental way.
Return to Chapter 4
Table of Contents
This site was hosted by the NASA Ames Research Center from 1994-2018 and is now hosted by:

 g, which experience must
determine. The habitable volume is that volume where
g, which experience must
determine. The habitable volume is that volume where  g/g is less than or equal to some number
which the study group calls the habitability parameter,
g/g is less than or equal to some number
which the study group calls the habitability parameter, 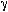 =
=  g/g. It is not
inconceivable, for example, that ways may be found to live safely
and comfortably through the entire range from 0 to 1 g. In that
case
g/g. It is not
inconceivable, for example, that ways may be found to live safely
and comfortably through the entire range from 0 to 1 g. In that
case 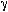 would equal 1, and the entire volume of the
space colony is habitable.
would equal 1, and the entire volume of the
space colony is habitable. .
This is just
.
This is just 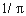 the total skin area of a
torus. Note that if the torus is spun so that there is 1 g of
pseudogravity at the outermost surface, and if the aspect ratio,
the total skin area of a
torus. Note that if the torus is spun so that there is 1 g of
pseudogravity at the outermost surface, and if the aspect ratio,
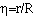 , is greater than the habitability
parameter,
, is greater than the habitability
parameter, 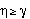 , and the above formula is sufficient. For a
rotating sphere the projected plane of usable area is the surface
of a cylinder inscribed in the sphere
, and the above formula is sufficient. For a
rotating sphere the projected plane of usable area is the surface
of a cylinder inscribed in the sphere 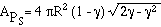
 .
. the expression for
the maximum can be used. (Alternatively, for smaller
the expression for
the maximum can be used. (Alternatively, for smaller 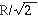 to maximize the available area). For a cylinder
of radius R and length L the projected area is just the surface
area
to maximize the available area). For a cylinder
of radius R and length L the projected area is just the surface
area 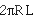 <.
<.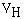
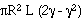
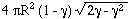
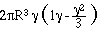
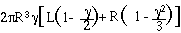
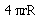
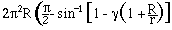
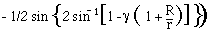
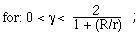 <
<